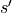The document itself is available locally.
Errata corrected in this version (relative to the official version held at
the JHU library) are detailed below.
The slide deck from my defense is
available in PDF form.
In addition to the thesis document itself, an addendum is available, containing a more fully fleshed-out
variant of the EarthBound algorithm of chapter 2.
Abstract:
We investigate the design of an expressive, purely-declarative, weighted logic programming language, Dyna. Dyna is a decade-plus effort in pushing the boundaries of declarative programming and “executable mathematics;” it instantiates an unusual point in the design space, as it is both Turing-complete (unlike Datalog) and devoid of a specified execution order (unlike Prolog). That is, it is designed to be, at once, both highly expressive and rich in opportunities for automated optimization. This thesis contains two major thrusts. We first consider both the denotational (§2.1.2 and §3.1.4) and operational aspects (§2.2 to §2.5, §3.2 to §3.6, and §4) of Dyna. In particular, for operational semantics, we introduce (§2.2) and extend (through §2.5) our EarthBound solver for finite circuits; §3 considers the generalization to logic programs proper. We then turn our attention to the static analysis of this language, considering mechanisms for reasoning both about abstract notions of well-formedness of programs (§5.2) as well as more mundane concerns of realizability of programs in actual computation (§5.3 and §5.4). Along the way we endeavour to place our work in the context of the larger field of logic programming languages and present our current thoughts on future avenues of exploration.
BibTeX:
@PhDThesis{filardo:dyna2,
author = {Nathaniel Wesley Filardo},
institution={Johns Hopkins University},
year = {2017},
month = {10},
title = {Dyna 2: Towards a General Weighted Logic Language}
}
Errata¶
The definition of idempotence in “Properties of Functions of Bags” in section 1.3 used
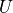 rather than
rather than 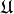 .
.Footnote 19, in Algebraic Structures, in section 1.3, has been corrected to include the overlooked case of equivalent elements
 and
and 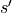 .
.The formula, in section 1.4, following “(recursively) considering the refutation” erroneously contained
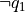 , which should have
been substituted away.
, which should have
been substituted away.In 2.2.1, “item (or, later, set) of items whose” has been corrected to “item (or, later, set of items) whose”.
It has been pointed out that the prose in 2.2.4.1 has a reading suggesting that
FreelyManipulateMcan directly delete a memo. The intent, as, thankfully, correctly captured by the code listing, is thatFreelyManipulateMusesFlushto update the memo table, thereby preserving Invariant 4. As no small edit would suffice, we hope that apologetic forewarning here in the errata is sufficient.At the end of 2.3.4, the word “information” was missing.
A small typographical error has been corrected in 2.3.5.3, with no impact to the meaning of the prose.
A small grammatical error has been corrected in 2.4.3, with no impact to the meaning of the prose.
Example 16 in 2.5 has been corrected; the old prose had the right setup but contained errors in the development of the story.
Years after writing this document, I was made aware of the 1989 paper “C-expressions: a variable-free calculus for equational logic programming” by Marco Bellia and M. Eugenia Occhiuto (https://www.sciencedirect.com/science/article/pii/030439759390170X and available without a paywall at https://core.ac.uk/download/pdf/81948651.pdf) which develops a formalism very similar to that of
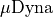 in section
3.1 and as considered again in chapter 4. For my oversight in not finding
this work in my literature survey, I can only apologize profusely.
in section
3.1 and as considered again in chapter 4. For my oversight in not finding
this work in my literature survey, I can only apologize profusely.In 3.2.1, range restriction is equivalent to
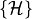 -SRR,
not the nonsensical
-SRR,
not the nonsensical 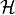 -SRR.
-SRR.3.2.1.2 was missing a closing parenthesis in prose.
The proof of Lemma 2 in section 3.3.4 contained a typo: “becoming equal when
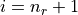 ” had a
” had a 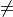 in the submitted version.
Thankfully, the lemma body itself is stated correctly.
in the submitted version.
Thankfully, the lemma body itself is stated correctly.In 3.4.2.2,
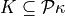 and not, as erroneously
stated,
and not, as erroneously
stated, 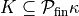 .
.In 3.4.2.2, a
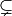 was erroneously entered as
was erroneously entered as 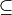 .
.In figure 5 of 3.4.3.2,
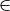 was missing its TeX backslash.
was missing its TeX backslash.In 3.4.4.2, syntactic nonsense was given when the term
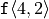 was meant.
was meant.The last paragraph before 3.6.2.1 had an erroneous cross-reference command.
In the discussion of Abstract Unification in 4.4.1.1, a TeXnical error resulted in
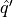 being rendered as
being rendered as 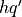 .
.In 4.4.3, the prose has been corrected to read “If we then remove
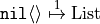 ”,
rather than proposing the removal of the just-added
“
”,
rather than proposing the removal of the just-added
“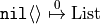 ”.
”.Theorem 3 in 5.3.2.3 contained a pair of typos: the functions
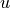 and
and  were erroneously rendered as
were erroneously rendered as 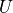 and
and 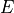 .
.Equation 5.10 in 5.3.5 had a
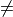 which should have been a
which should have been a
 .
.In 5.4,
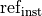 should have read
should have read
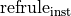 .
.In 6.1.1, the example was of the correct general shape, but used incorrect values, which have now been corrected.
In 6.2, an erroneus “we assume that all such sets are disjoint” has been stricken and replaced with the intended “these do not include any inherited rules.”
In 6.4, it was omitted that
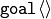 was to be
summed to obtain the result given.
was to be
summed to obtain the result given.In the addendum,
Driveused in its loop when it should have
been using
in its loop when it should have
been using